OLASILIK ve OLASILIK ÖĞRETİMİ ÜZERİNE BİR ÇALIŞMA
Levent ÖZBEK[1]
GİRİŞ
Evrende olup bitenleri anlama ve anlatma çabası içinde olan insan, ilgilendiği olay ve süreçlerle ilgili çeşitli modeller kurarak bu modeller üzerinde gelecekte ne gibi durumlar ortaya çıkabileceğini bilmeye çalışır.
Newton’un Mekaniği ile doruk noktasına ulaşan Laplace anlamında belirlenimci dünya görüşü (determinizm-gerekircilik, saat gibi tıkır-tıkır işleyen evren modeli) kuantum fiziğinin gelişimi ile beraber yerini olasılıkçı dünya görüşüne bırakmak zorunda kalmıştır. Reaktörler için ya da atomların ışıması için olasılık hesapları yapılır ve gözlemlerle uyuşan sonuçlar bulunur. Bu anlamda belirlenimcilik kuantum mekaniğinde vardır ama Laplace anlamında belirlenimci değildir [19]. Belirlenimci dünya görüşü ve bununla ilişkili nedensellik ve rastlantı kavramları bilim, felsefe, sanat gibi alanlarda çok tartışılan konular arasında yer almaktadır [1]-[4].
Psikologlar kesinlik arayışını, çocukluğun ilk günlerine, kişinin henüz kuşku duygusundan tedirgin olmadığı, ana-babanın sağladığı güven içinde rahat olduğu günlere bir dönüş arzusu olarak açıklamaktadırlar. Bu arzu genellikle, çocuğu, kuşkulanmayı bir günah, güven duymayı dinsel bir buyruk saymaya koşullandırılan bir eğitim tarafından yoğunlaştırılır. Kesinlik arayışı, hataya yol açan en tehlikeli kaynaklardan biridir; çünkü, bu eğilim üstün bilgi edinme çabası ile birlikte gider [5].
Olasılık kavramı, bilgi problemlerinin en önemlileri ile ilgilidir. Olasılık her şeyden önce doğa yasalarında kendini gösterir [6]. Olasılık ve olasılık kavramlarının diğer bilim alanlarındaki kavramlarla olan ilişkilerini değişik biçimlerde ele alan pek çok popüler yayın bulunmaktadır [12]-[18].
Eğitim sürecinde olasılık kavramlarının yeterince öğretilememesi önemli problemlerden birisidir ve bununla ilgili yapılan çalışmalar günümüzde tüm ülkelerde devam etmektedir. Bununla birlikte ülkemizde ve diğer ülkelerde olasılık kavramlarının öğretiminde çeşitli nedenlerle zorluklar yaşandığı, öğretimin etkin bir şekilde yapılamadığı birçok araştırmacı tarafından belirtilmektedir [7]-[11].
Bulut ve diğ. [7], olasılık öğretiminde karşılaşılan sorunların başında öğretim materyallerinin eksikliği olduğunu vurgulamış ve olasılık kavramlarının öğretiminde kullanılacak çalışma yapraklarının geliştirilmesine yönelik çalışma yapmışlardır. Truran [9], olasılığı öğretirken simetrinin sık kullanıldığı madeni para ve zar atışı örneklerini ele alarak çeşitli yaş gruplarındaki çocukların olasılıkla ilgili düşüncelerini belirlemek amacıyla araştırma yapmıştır. Olasılık kavramının yaşla birlikte değişik görünümler gösterdiğini, oyunların basit deneylere göre daha etkili olduğunu saptamıştır. Sonuç olarak çeşitli yaş gruplarında yaptığı röportajlardan, çocuklardaki olasılık kavramının gelişmesinin tamamen anlaşılamadığını ve hangi öğretim yöntemlerinin daha iyi olduğu konusunda bu görüşmelerin yeterince ipucu vermediğini belirtmiştir. Batanero ve diğ. [11], rasgelelik kavramının tarihsel boyutunu ele alarak bu kavramın öğretiminde karşılaşılan sorunlar ile ilgili araştırma yapmışlardır.
Bu çalışmanın birinci bölümünde, olasılığın anlamı üzerindeki görüşler ile ilgili bilgi verilmiştir. İkinci bölümde, olasılık kavramının öğretiminde dikkat edilecek konulara değinilmiştir. Üçüncü bölümde, olasılık kavramının anlaşılmasına yönelik bilgisayar destekli benzetim uygulamaları ile ilgili bir örnek üzerinde durulmuştur.
-
Olasılığın Anlamı
Rasgelelik ve bununla bağlantılı olan olasılık kavramının çerçevesinin kolay oluşmadığı, bu konuda öğretim gören öğrenciler tarafından da dile getirilmektedir [20]. Klasik olasılık kuramına göre, sayısal olasılık değeri, “uygun sonuçlar” sayısının, “tüm sonuçlar” sayısına bölümü olarak tanımlanır. Bu tanım, öznel ve nesnel diye adlandırılan farklı yorumlara yol açmaktadır. “Hilesiz bir zarla 6 atmanın olasılığı 1/6’dır” önermesi sayısal olasılık önermesine bir örnektir. Sorun, sayısal bir olasılık önermesinin nasıl yorumlanacağıdır.
Popper [21], öznel yorumlamada bazı ruhbilimsel öğelerin olduğunu, buna göre olasılık derecesini kesinlik ya da belirsizlik inancının ölçütü olarak değerlendirmiştir. Reichanbach [5], rasyonalistler için, olasılık derecesi denen şey, nedenlerin yokluğunda aklın ürünüdür, değerlendirmesini yapmıştır. Popper [21], nesnel yorumlamayı ise, sayısal her olasılık önermesi, olaylar dizisi içerisindeki belirli olayların göreli sıklığına ilişkin bir önerme olarak nitelemiştir. Böylece örneğin, “bir sonraki zar atışında 1 atmanın olasılığı 1/6 dır” biçimindeki bir önerme, bir sonraki zar atışının bir önermesi değil, atışlar kümesinin tamamının bir önermesidir; bir sonraki atış ile ilgili bir önerme de bu kümenin bir elemanıdır; bu önerme yalnızca, söz konusu kümede “1 atmanın” göreli sıklığının 1/6 olduğunu ileri sürmektedir. Bu yaklaşıma göre, sayısal olasılık önermeleri, ancak sıklığa ilişkin bir yorum yapılabildiğinde kabul edilebilir.
Olasılıklar hesabındaki başlıca önermelerin geçerliliğini sağlayan bir sıklık kuramı R.V. Mises tarafından ortaya konulmuştur. Reichanbach [5], bu kuramı olasılığın empirist (deneysel) felsefesi olarak adlandırmıştır ve rasyonalist yorumun bilimsel felsefede yer almaması gerektiğini söylemiştir. Bu kurama göre olasılıklar hesabı, belirli “rasgelelik” öğesi içeren olaylar dizisinin bir kuramıdır. Bu olaylar dizisini tanımlayan iki belitsel koşul vardır: Bunlar, “sınır-değer beliti” ve “gelişigüzellik belitidir”. Bir olaylar dizisi bu iki koşulu doyurduğunda, Mises bunu, sonsuz biçimde yinelendiği düşünülen denemeler dizisi – yani “kolektif”- olarak tanımlamaktadır. Örneğin, yıpranmayan bir zarla yapılan atışlar dizisi bir kolektifdir. Bu tür her olayın belirli bir özelliği vardır; örneğin “beş atış” bir özelliktir. Olaylar dizisindeki her bir eleman için yeni bir dizi “göreli sıklıklar dizisi” karşılık getirilebilir. Özellikler dizisi uzadıkça, sınır-değer belitine göre, göreli sıklıkların dizisi belirli bir sınır değere ulaşmalıdır. Mises’e göre “olasılık” sözcüğü, bir “kolektifin içinde bulunan göreli sıklığın sınır-değerinin” başka bir ifadesidir. Mises’e göre olasılık hesabının tek amacı şudur: Verilmiş olasılıklardan yola çıkarak, başka olasılıkların hesaplanmasıdır. Reichanbach [5], olasılığın sıklık yorumunun, bir olasılık önermesinin tek bir olaya uygulanması sırasında güçlük çıkaracağını, tek bir olayın olasılığının sıklık olarak belirtmenin bir anlam taşımadığını söylemiştir.
Olasılığın çağdaş tanımı matematiğin alt dalı olan ölçü teorisindeki kavramlar yardımıyla Kolmogorov tarafından verilmiş böylelikle olasılık teorisi aksiyomatik bir yapıya kavuşturulmuştur. Bu tanım, klasik olasılık tanımını da içermektedir. Olasılığın bu tanımı [22]’ de bulunabilir. Olasılık teorisi Kolmogorov Aksiyomları olarak bilinen matematiksel alt yapısı ve Mises’in sıklık kuramı ile birlikte ele alınmakta ve rasgelelik içeren süreçleri modellemede kullanılmaktadır.
Mises’in sıklık kuramı, Bernouilli Büyük Sayılar Kuralı ile matematiksel olarak daha iyi anlaşılabilir. Büyük Sayılar Kuralı kuramsal ve deneysel iki sayıyı birbirine bağlamaktadır. Bu kuralın aracılığı ile olasılık teorisi deneysel çalışma ile temas eder ve bu kuramın teorik olarak elde edilen sonuçları çeşitli deneysel bilim dallarına uygulanarak doğanın daha derin, ama kesin yasalarla ifade edilemeyen kanunlara uygunluklarını matematiksel olarak ifade etmeye olanak sağlar. Bernouilli Teoremi olarak bilinen bu kural [23]’de verilmiştir.
-
Olasılık Öğretimi ve Öneriler
İnsanlar doğal olarak kesinlik arayışı içindedirler. Kuşku duyma ise belirsizliği beraberinde getirir ve sonradan kazanılan bir davranış biçimi olarak görülebilir. Kişide kuşku duyma eğiliminin ortaya çıkması ile bu kavram sezgisel olarak oluşmaya başlar.
Olasılık öğretiminde karşılaşılan sorunlar dikkatli bir şekilde ele alınmalıdır. Öğrencilerin “olasılık” ve “rasgelelik” kavramları hakkındaki düşüncelerini öğrenmek amacıyla çeşitli yaş gruplarını içine alan araştırmalar yapılmalı ve bu doğrultuda öğretim yöntemleri geliştirmek için çalışmalar başlatılmalıdır.
Özellikle eğitim fakültesi öğrencilerine bu konular anlatılırken konunun teknik yönü kadar tarihi ve felsefi içeriğine de yer verilmelidir.
Olasılığın değişik bilim dalları ile olan ilişkileri üzerinde durulmalı bunlara uygun modeller anlatılmalıdır.
Olasılığın tümdengelimci (aksiyomatik kuram) ve tümevarımcı (sıklık kuramı) boyutu beraber ele alınmalıdır. Anlatılan konu ile ilgili deneysel çalışmalara yeterince yer ayrılmalıdır. Öğrencilerin kendi kendilerine deney yapmaları sağlanmalıdır.
Bilgisayar destekli uygulamalardan yararlanılmalıdır. Buna uygun ders programları geliştirilmeli öğretmene ve öğrenciye yol gösterecek kitaplar hazırlanmalıdır.
-
Olasılık Öğretiminde Deney ve Benzetim
Kurulan model üzerinde deney yapmaya benzetim denir. Bazı deneylerin yapılmasının zorluğu veya başka nedenlerle olasılık öğretiminde bilgisayar destekli benzetimden yararlanılır. Ayrıca bilgisayarda verilecek grafik ve hareketli görüntüler de problemin anlaşılmasına yardımcı olabilir. Bu amaçla, aşağıda verilen problem için model kurulmuş ve bu model üzerinde benzetim çalışması yapılmıştır.
Problem:
Deney; içinde 2 kırmızı, 3 sarı top bulunan bir torbadan çekilen topu tekrar torbaya atmak koşulu ile 100 top çekip gelen kırmızı topların sayısının gözlenmesi olsun. Problem de 100 top çekilişinde beklenen kırmızı topların sayısının ne olacağı olsun.
Model kurma:
Kırmızı ve sarı topların sayısı bilindiğinden klasik olasılık tanımını kullanılarak, kırmızı top gelmesi olasılığı için P(k)=2/5, sarı top gelmesi olasılığı için de P(s)=3/5 alınabilir. Öğrenci sezgisel olarak (rasgele değişken, olasılık dağılımları, Bernouilli Dağılımı, Binom Dağılımı, beklenen değer,… gibi kavramları bilmese bile) 100*2/5 gibi basit bir aritmetik işlem yaparak sonucu söyleyebilecektir. Bu düşüncenin altında yatan da olasılıkların yukarıdaki gibi seçilmesi yani modellenmesidir.
Deney :
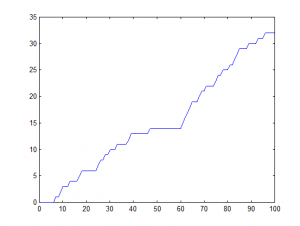
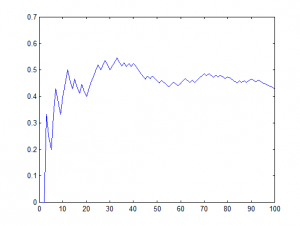
Sınıfta bulunan öğrenciler ikişerli gruplara ayrılıp sözü edilen benzer torbalar dağıtılarak her grubun deneyi yapması ve deneyler bittiğinde de sonuçları karşılaştırmak amacıyla tahtaya yazmaları istenir. Deney sonuçları ile sezgisel olarak bulunan sonuçlar karşılaştırılır. Eğer kurulan model doğruysa deney sonuçları modelin verdiği sonucu destekleyecektir (yakın çıkacaktır). Her grup yaptığı deney sonuçlarını x-ekseni deney sayısı (deney sıra numarası), y-ekseni de o deney sayısına kadar gelen kırmızı topların sayısını işaretlemek üzere Şekil-1’deki gibi bir grafik üzerinde gösterdiğinde kurulan modelin geçerliliği için sezgi sahibi olabilir. Yine benzer şekilde y-ekseninde gelen kırmızı topların sayısının deney sayısına oranlanmasından bulunan sonuç gösterilirse Şekil-2’deki gibi istatistik teorisinin temelinde yatan Büyük Sayılar Yasasının anlamı konusunda sezgi sahibi olabilir.
Şekil-1: Kırmızı topların sayısı
Şekil-2: Kırmızı topların sayısının deney sayısına oranı
Deney çok zaman alacağından veya başka nedenlerle birkaç gruba yaptırmakla yetinilebilir. Böyle bir durumda bilgisayarda deney istenildiği kadar tekrarlanabilir.
Benzetim:
Bu deneyi bilgisayarda gerçekleştirmek için çeşitli programlama dilleri kullanılarak program yazılabilir. Her programlama dilinde bulunan ve sayı üretmek için kullanılan (rnd, rand, random,… gibi) fonksiyon yardımıyla deney; Eğer RAND<2/5 koşulu sağlandığında kırmızı top çekildi, aksi durumda sarı top çekildi biçiminde yapılabilir. Bu deneyi bilgisayarda n kez gerçekleştirmek amacıyla aşağıdaki Matlab programı kullanılabilir. Program çalıştırıl-dığında Şekil-1’dekine benzer bir grafik verecektir. n sayısı değiştirilerek deney istenildiği kadar tekrarlanabilir. Ayrıca, programda 12.satır,
x(deneysay)=kırmızısay/deneysay;
satırı ile değiştirilerek Şekil-2’dekine benzer bir grafik elde edilebilir. Bu benzetim uygulamasında dikkat edilecek konulardan birisi
Eğer RAND<2/5 ise kırmızı
Koşulunun yazılmasının kurulan modelden ( P(k)=2/5 ) gelmesidir.
-
clc
-
clear
-
n=100;
-
for deneysay=1:n
-
x(deneysay)=0;
-
end
-
kırmızısay=0;
-
for deney-say=1:n
-
if rand<2/5
-
kırmızısay=kırmızısay+1;
-
end
-
x(deneysay)=kırmızısay;
-
end
-
plot(x)